14e Championnat International des Jeux Mathématiques et Logiques
1/4 de finale individuels
Date limite: 31 décembre 1999.
Catégories
Énoncés des problèmes
Début catégorie CM
- 1 - Le Xième X
(coefficient 1)
- Mathias écrit les nombres entiers en toutes lettres, dans l'ordre,
à partir de un:
UN DEUX TROIS QUATRE CINQ SIX SEPT HUIT...
Le dixième E
écrit apparaît dans QUINZE
et le dixième
U
dans DIX-NEUF
.
Mais dans l'écriture de quel nombre le dixième X
apparaît-il?
- 2 - Les 8 nombres
(coefficient 2)
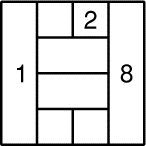
Mathilde prétend qu'il est possible de placer les nombres de 1 à 8 dans
les cases du tableau ci-contre de façon que deux nombres qui se suivent
(comme 3 et 4 par exemple) ne soient jamais situés sur deux cases qui se
touchent. Mathias a déjà placé les nombres 1, 2 et 8.
À vous de placer les 5 autres!
Début catégorie C1
- 3 - La tarte carrée
(coefficient 3)
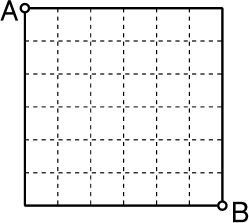
C'est aujourd'hui l'anniversaire de Mathias. Sur la table, il y a une
superbe tarte carrée. Il faut la partager en trois parts de même poids, en
donnant deux coups de couteau rectilignes passant l'un par le point A
et l'autre par le point B. Faites le partage.- 4 - La vieille calculatrice
(coefficient 4)
- Ma vieille calculatrice ne peut plus faire que deux opérations:
ajouter 12 au nombre affiché, ou bien lui soustraire 7. Aujourd'hui,
elle affiche 1999.
En combien d'opérations, au minimum, pourrai-je faire apparaître le
nombre 2000 sur l'écran?
Début catégories C2 L1 GP L2 HC
- 5 - Histoire de billes
(coefficient 5)
- Mathilde a deux billes de plus que Mathias. Le nombre de billes
de Mathias est le double du nombre de billes de Matthieu. Matthieu a
sept billes de moins que Mathilde.
Combien ont-ils de billes à eux trois?
- 6 - Le carreleur américain
(coefficient 6)
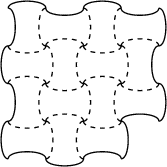
Tom, carreleur originaire des Amériques, fabrique lui-même les
carreaux
qu'il utilise.
Aujourd'hui, il a fabriqué cinq carreaux
identiques pour
carreler
la forme ci-contre. Les bords des carreaux, qui ne
peuvent être retournés, suivent les lignes du quadrillage
.
Retrouvez la position des cinq carreaux.
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - Autoréférence
(coefficient 7)
| Dans ce cadre, il y a ......................
consonnes de plus que de voyelles. |
Complétez le cadre ci-contre à l'aide d'un nombre écrit en toutes
lettres, de telle sorte que la phrase qu'il contient soit vraie.- 8 - La furibarde
(coefficient 8)
- Le
lapgourou
est un animal qui court en ligne droite
de la manière suivante: il met 2 secondes pour faire un saut de
4 m, il se repose une seconde et
il recommence à sauter.
La furibarde
est un animal qui saute moins loin; elle met une
seconde pour faire un bond de 3 m,
mais elle ne s'arrête pas entre les bonds.
La furibarde est à 32 m du lapgourou
qu'elle décide de poursuivre. Elle ne peut capturer le lapgourou que
lorsqu'il est arrêté.
Dans combien de secondes, au maximum, pourra-t-elle le faire?
- 9 - Chaîne de dominos
(coefficient 9)
- Philippe possède un jeu complet de 28 dominos (du 0-0 au 6-6).
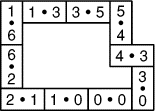
Sa soeur Sophie lui a subtilisé les 7 dominos comportant un 6 (de 0-6 à
6-6). Qu'à cela ne tienne! Philippe décide de former une chaîne fermée
avec les dominos restants, en respectant la règle du jeu de dominos. On
rappelle que deux dominos ne peuvent être mis en contact que par un côté
portant le même nombre de points (voir l'exemple donné ci-contre avec 10
dominos).
Quelle sera le nombre maximum de dominos utilisés par Philippe pour
former une chaîne fermée?
Fin catégorie C1
- 10 - Téléphone
(coefficient 10)
- Lorsque Pierre demande à Marie son numéro de téléphone pour pouvoir
l'appeler, celle-ci répond:
Comme tous les numéros de téléphone français, il est formé de
10 chiffres que l'on a l'habitude de grouper par deux. Les dix chiffres
sont tous différents, et chaque groupe de deux chiffres est supérieur à
la somme de tous les groupes précédents. De plus, si l'on considère le
nombre que forme ce numéro, c'est le plus petit possible.
Quel
est le numéro de téléphone de Marie?
Note: on rappelle qu'en France le premier chiffre d'un numéro de
téléphone est le 0 (opérateur téléphonique) et le second est compris
entre 1 et 6 inclus (pour les particuliers comme Marie tout du
moins).
- 11 - Le masque inca
(coefficient 11)

Des recherches archéologiques viennent de révéler à nos yeux émerveillés
un masque inca en or pur. Le plan de ce masque est représenté ci-contre
sur un plan quadrillé.
Calculez l'aire de ce masque, l'unité d'aire étant l'aire d'un petit
carreau. On n'oubliera pas de déduire l'aire des yeux, de la bouche,
du nez et des sourcils. Pour d'éventuels calculs, on prendra 355/113 pour
π.
Fin catégorie C2
- 12 - La fraction
(coefficient 12)
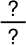
On choisit le numérateur et le dénominateur, qui peuvent être
égaux ou différents, de la fraction ci-contre dans l'ensemble
{1 ; 2 ; 3 ; 4 ; 5 ; 6}.
Combien de valeurs différentes la fraction peut-elle prendre?
Remarque: 2 / 1 est une fraction.- 13 - Le couple parfait
(coefficient 13)
- Deux nombres se marient pour former un nouveau nombre. Un couple de
nombres entiers plus grands que 0 est dit parfait si chacun des nombres
est un carré parfait ainsi que le nombre obtenu en les juxtaposant. Ainsi,
(324 ; 9) est le plus petit couple parfait supérieur à 1999, car
324, 9 et 3249 sont des carrés. Combien il y a-t-il de couples parfaits
inférieurs à 1999? Donnez-en deux.
- 14 - Le carré et le rectangle
(coefficient 14)
- Un rectangle dit à un carré:
Tiens, nous avons des diagonales
égales
.
_ Certes
, répond le carré, mais
j'ai une aire de 144 cm²,
tout le monde ne peut pas en dire autant!
_ Voyons cela
, rétorque le rectangle, en
appliquant une de ses diagonales sur une diagonale du carré.
Tous deux constatent alors que leur partie commune a une aire de
96 cm².
Quelle est l'aire du rectangle?
Fin catégories L1 GP
- 15 - Les briques de Mark Ov
(coefficient 15)
- Les briques de Mark Ov sont des parallélépipèdes rectangles ne
possédant aucune face carrée. Les dimensions de chaque brique sont
entières, dans une certaine unité. De plus, ces briques présentent la
particularité que la somme des carrés de leurs trois dimensions est égale
au triple de leur produit, à l'instar du cube de côté unité. Un exemple
d'une telle brique est (2 ; 5 ; 29), puisque
2² + 5² + 29² = 3 × (2×5×29) = 870.
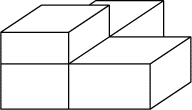
La figure ci-dessus, qui ne respecte pas les proportions, montre quatre
briques de Mark Ov assemblées en coin. Pour chacune des trois surfaces de
contact, les deux dimensions de chacune des deux briques correspondent
exactement.
Si les quatre briques sont toutes différentes les unes des autres, quel
est le volume minimum de la plus volumineuse d'entre elles?
- 16 - Le carré dans la petite larme
(coefficient 16)

La petite larme
représentée ci-contre est formée de deux
demi-cercles de rayon 5 cm et
d'un demi-cercle de rayon 10 cm.
On place 4 points A, B, C, D sur le pourtour de cette petite larme de
telle sorte que ABCD soit un carré.
Quelle est l'aire de ce carré?
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org